Hopfield neural network for artificial intelligence machine learning

The neural network revived in the 1980s thanks to the physicist John Hopfield. In 1982, Hopfield proposed a new neural network that can solve a large class of pattern recognition problems, and can also give an approximate solution to a class of combinatorial optimization problems. This neural network model is later called the Hopfield neural network.

Hopfield neural network is a kind of cyclic neural network [please refer to the artificial intelligence of the public number "Science-optimized life" (23)], invented by John Hopfield, who introduced the related ideas (kinetics) of physics to neural networks. The structure is thus formed by the Hopfield neural network. In 1987, Bell Labs successfully developed a neural network chip based on the Hopfield neural network.

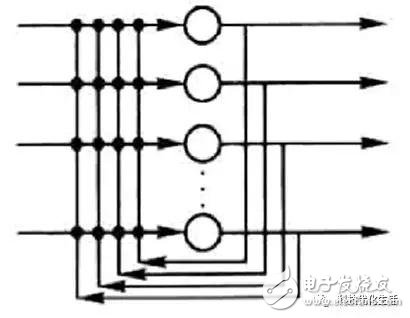
The Hopfield neural network is a recurrent neural network with feedback connections from the output to the input. Each neuron is connected to all other neurons, also known as a fully interconnected network.

Hopfield Neural Network Overview:

Hopfield neural network HNN (Hopfiled Neural Network) is a neural network that combines storage systems and binary systems. It guarantees a very small convergence to the local, but converges to the wrong local minimum, rather than a global minimum. Hopfield neural networks also provide models that mimic human memory.

The Hopfield neural network is a feedback neural network, and its output is fed back to its input. Under the input excitation, its output will produce constant state changes. This feedback process will be repeated. If the Hopfield neural network is a convergent stable network, the variation of this feedback and iterative calculation process becomes smaller and smaller. Once the stable equilibrium state is reached, the Hopfield network will output a stable constant value.

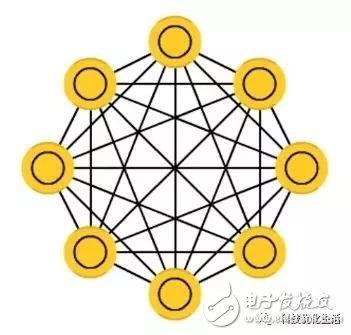
For a Hopfield neural network, the key is to determine its weight coefficient under stable conditions.

Hopfield neural networks are divided into two types: 1) discrete Hopfield neural networks; 2) continuous Hopfield neural networks.

Discrete Hopfield Neural Network:

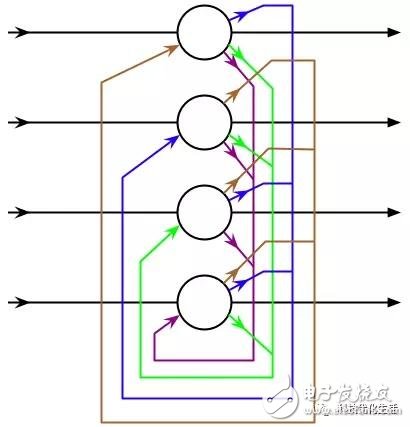
The earliest proposed network of Hopfield is a binary neural network. The excitation function of each neuron is a step function or a bipolar function. The input and output of the neuron only take {0, 1} or { -1, 1}, so It is called Discrete Hopfieldd Neural Network (DHNN). In DHNN, the neurons used are binary neurons; therefore, the discrete values ​​1 and 0 or 1 and -1 output indicate that the neurons are in an activated state and a suppressed state, respectively.

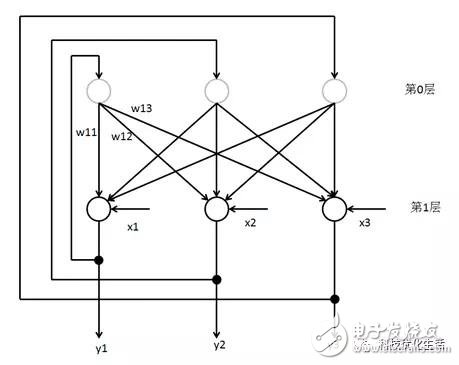
The discrete Hopfield neural network DHNN is a single-layer network with n neuron nodes, and the output of each neuron is input to other neurons. There is no self-feedback for each node. Each node can be in a possible state (1 or -1), that is, when the stimulus to which the neuron is subjected exceeds its threshold, the neuron is in a state (such as 1), otherwise the neuron is always In another state (such as -1).

DHNN has two ways of working:

1) Serial (asynchronous) mode: At time t, only the state of a certain neuron j changes, while the state of other n-1 neurons does not change, which is called serial working mode. And have:

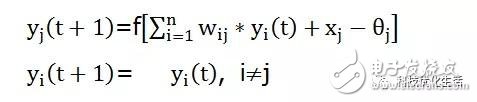
2) Parallel (synchronous) mode: At any time t, all neurons have changed state, called parallel working mode. And have:

DHNN stability:

Suppose a DHNN whose state is Y(t):

If for any Δt "0", when the neural network starts from t = 0, there is an initial state Y (0). After a limited time t, there are:

Y(t+Δt)=Y(t)

The DHNN network is considered to be stable, and its state is said to be stable. The steady state X of the DHNN network is the attractor of the network for storing memory information. The stability in serial mode is called serial stability; the stability in parallel mode is called parallel stability.

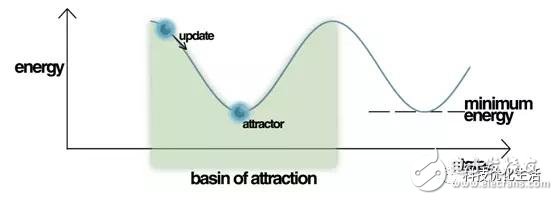
DHNN is a multi-input, binary-valued nonlinear dynamic system with thresholds. In a dynamic system, equilibrium steady state can be understood as some form of energy function (energy funcTIon) in the system, its energy is continuously reduced, and finally at the minimum.

Sufficient condition for DHNN stability: If the weight coefficient matrix W of DHNN is a symmetric matrix and the diagonal element is 0, then the network is stable. That is, in the weight coefficient matrix W, if:

Then the DHNN is stable.

W is a symmetric matrix is ​​only a sufficient condition, not a necessary condition.

DHNN associative memory function:

An important function of DHNN is that it can be used for associative memory, namely associative memory, which is one of the intelligent features of human beings.

To achieve associative memory, DHNN must have two basic conditions:

1) The network can converge to a stable equilibrium state and use it as a sample of memory information;

2) Have the ability to recall and be able to recall the complete memory information from a certain piece of information.

DHNN implements the associative memory process in two phases:

1) Learning and memory stage: The designer determines a set of appropriate weights through a design method, so that DHNN remembers the desired stable balance point.

2) Lenovo recall stage: DHNN's work process.

Memory is distributed, and association is dynamic.

For DHNN, chaos is not possible due to the limited network state.

DHNN limitations:

1) the limited capacity of memory;

2) association and memory of pseudo-stable points;

3) When the memory samples are close, the network cannot always recall the correct memory, etc.;

4) DHNN balance stability point can not be set arbitrarily, and there is no universal way to know the equilibrium stability point in advance.

Continuous Hopfield Neural Network:

The continuous Hopfield neural network (CHNN) and the DHNN are identical in topology.

CHNN stability:

CHNN stability conditions require:

CHNN differs from DHNN in that its function g is not a step function but a continuous function of the S type. Generally take:

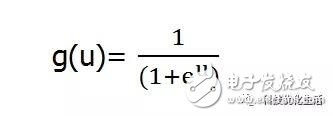
CHNN is continuous in time, so each neuron in the CHNN network is working in a synchronous manner.

When the neuron transfer function g of the CHNN network is continuous and bounded (such as the Sigmoid function), and the weight coefficient matrix of the CHNN network is symmetric, then this CHNN network is stable.

Optimization:

In practical applications, if the optimization problem can use the energy function E(t) as the objective function, then the CHNN network directly corresponds to the optimization problem. In this way, a large number of optimization problems can be solved using the CHNN network. This is also the basic reason why the Hopfield network is used for neural computing.

The main difference between CHNN and DHNN:

The main difference between CHNN and DHNN is that the CHNN neuron activation function uses the Sigmoid function, while the DHNN neuron activation function uses the hard limit function.

Hopfield neural network application:

Early applications of Hopfield neural networks include content-addressable memory, analog-to-digital conversion, and optimized combination calculations. It is representative to solve the TSP problem. In 1985, Hopfield and Tank used the Hopfield network to solve the TSP problem of N=30, thus creating a new way of neural network optimization. In addition, Hopfield neural networks are widely used in artificial intelligence machine learning, associative memory, pattern recognition, optimization computing, VLSI and parallel implementation of optical devices.

Conclusion:

Hopfield Neural Network (HNN) is a neural network with cyclic and recursive properties combined with storage and binary systems. Invented in 1982 by John Hopefield. For a Hopfield neural network, the key is to determine its weight coefficient under stable conditions. Hopfield neural networks are divided into discrete and continuous types. The main difference lies in the difference of activation functions. The Hopfield Neural Network (HNN) provides a model for simulating human memory. It has a wide range of applications in artificial intelligence machine learning, associative memory, pattern recognition, optimized computing, parallel implementation of VLSI and optical devices.

DC Permanent Magnet Gear Motor

Dc Motor,24V Dc Gear Motor,Electric Gear Motor,Dc Permanent Magnet Gear Motor

NingBo BeiLun HengFeng Electromotor Manufacture Co.,Ltd. , https://www.hengfengmotor.com