Special treatment is unclear: deep decryption of IBM black technology quantum computer

Lei Feng: press author: James Zhu, this article for you to introduce 1) the history of development of quantum computers; 2) the advantages of quantum computers over traditional computers; 3) the relationship between quantum algorithms and ours; 4) IBM Quantum online experience Service Introduction.

Isn't quantum computers really just in science fiction? What is the difference between it and ordinary computers? What is the relationship with ordinary programmers? This article is an embarrassing and unclear, I hope to take you to explore the quantum computer!

In 2001, IBM published an article saying that "in the next few decades, quantum computers will most likely come out of science fiction and scientific research laboratories (mainly at IBM)."

Now this sentence has become a reality, and it took only a dozen years. On Wednesday, IBM scientists disclosed the company’s quantum computer access cloud service to the public for the first time. The development of science and technology is always shocking. And IBM hopes to develop experimental chips for quantum computers within a few years. At present, IBM has not officially disclosed the quantum computing service, but interested friends can log in to IBM Quantum to apply for trial.

IBM is developing a general-purpose quantum computer based on the superconductivity effect of quantum logic gate architecture. For quantum computers, many media reports have been reproduced in the domestic market, but most of them basically remain at the level of translation of English media. And forwarded to each other, there are few trial evaluations of original or similar electronic products. The author of this article happens to do excessive sub-encryption research and experiments, and is also interested in quantum computing. Photonics, one of the author's majors, is also one of the physical implementations of quantum encryption/quantum computation.

Therefore, we have specially introduced a science introduction from shallow to deep, young and old, to explain to everyone the principles of quantum computers, and the difference between ordinary computers, and our programmers, and the author also uses IBM's open services to do Some evaluations. It is hoped that readers without any professional background will be able to glance at the leopards from this article, and they will also gain something for readers who have relevant background knowledge (mainly university physics, quantum mechanics, and digital circuits/analog circuits).

Stephen Wisner first proposed "computing equipment based on quantum mechanics" in 1969. A series of studies in the 1980s have enriched the theory of quantum computers. At a meeting of MIT physics and computer technology in May 1981, American physicist Richard Feynman, born in 1918, made a report “Simulating Physics With Computers”, unveiling research and development quantum. A new chapter in the computer.

In the report, Feynman proposed: Can a classical Turing computer be used to simulate quantum physics? The answer is no, using traditional computers to simulate quantum mechanics, the amount of computation will increase exponentially as the system (microscopic number of particles) increases. Feynman thinks that the essence of the microcosm is quantum. To simulate it, one has to use the same way as nature works, that is, the quantum method. Feynman first linked physics with computer theory. His brilliant speech at the MIT conference made computer scientists pay attention to the progress of physics and pay attention to quantum mechanics.

In 1994, Peter Shor, a Bell Labs expert, demonstrated that quantum computers can perform discrete logarithmic operations and that they outperform traditional computers.

On May 11, 2011, D-Wave Systems of Canada released a D-Wave One, a computing device known as "the world's first commercial quantum computer."

In May 2013, Google and NASA released D-Wave Two in a quantum artificial intelligence laboratory in California.

Quantum computing is a theoretical science. It is the science of how to directly apply quantum mechanical phenomena such as quantum superposition states and quantum entanglement states to the data. In the final calculation results, there is no difference between the quantum computer and the existing computer (otherwise, there must be one side that is wrong, and the wrong side has no practical value). The biggest difference between them is that there is a world of difference in computing , which will be explained in detail later.

There are three main types of quantum computing models:

Quantum circuit model

One-way quantum computing model

Adiabatic quantum computing model

Quantum circuit model

Quantum circuit model is to calculate the quantized computing process as a classical calculation, as well as different "logic gates" (of course, quantum operation) in the quantum state, and finally get the expected quantum state.

2. Unidirectional quantum computing model

The one-way quantum computation model transforms quantum computing into teleportatio and two dimensional cluster states so that we can obtain the quantum gate operation we want (quantum Gates).

3. Absolute thermal calculation model

The adiabatic quantum computation model is based on the problem of first classifying the problem into the Hamiltonian ground state of the complex Hamiltonian (that is, finding the ground state to find the final result), and then starting with a simple Hamiltonian. Finally, the required ground state is obtained through the adiabatic process.

Quantum computers were created and still needed good algorithms. Just like the sorting problem in our daily computer, a well-written algorithm can basically achieve O(nlog(n)) time complexity, and the bad algorithm is probably O(n^2).

To give a very practical example: Fast Fourier Transform (FFT) is a very common and very useful function in signal processing and image processing. Its time complexity is O(nlong(n)). With the aid of quantum computers, the complexity of the FFT can be reduced to O((log(n))^2), and even reading the O(n) time of the data is useless because only log(n) qubits can describe n Dimension vector. With high-performance FFT, the factorization complexity can reach sub-exponential time.

At present quantum computers have used the Shor's Algorithm to perform a prime decomposition of 15 in a scalable manner. Some people say that using the Shor algorithm to achieve the prime decomposition can be compared with the "Hello World!" in the classic computer. In addition to admiring its pioneering status, it also illustrates from a side that quantum computing is still in its infancy.

The relationship between the time complexity of quantum algorithms and big data:

With the above introduction, the eager readers should already be aware of the fact that the greater the amount of data, the more obvious the advantage of the quantum algorithm over time complexity: when n=1000, the traditional algorithm of O(n^2) needs One million steps are calculated, and O(nlog(n)) is slightly better. It also takes thousands of steps. Quantum computing takes only a few steps to complete the entire operation and get the final result.

In the era of big data, n=10000000 is commonplace, then the comparison on the top becomes 10^12 vs 10^6 vs 10^2, and the difference in time-consuming is several orders of magnitude.

The above is only taking FFT as an example. Actually, once a practical algorithm is found to achieve O(n) or even O(1) efficiency, the conventional electronic computer can be completed in the big data field.

Programmers who understand quantum algorithms will become more sought-after than current programmers who are familiar with deep learning algorithms and big data architectures.

So investing the necessary time and energy to learn a bit of quantum computing is a good choice for self-improvement. The IBM Quantum Experience website also provides this platform and opportunity.

The relationship between the time complexity of quantum algorithms and cloud computing:

Quantum algorithms are somewhat of a blow to the cloud storage industry. At present, all major powers are able to quietly study quantum computing in order to instantly decrypt important encrypted files. As long as this technology is mature and available, any cloud data stored in third parties will become insecure. Because even encrypted storage can be cracked in the blink of an eye.

With the threat of quantum computing, users will more conservatively store sensitive data in a physical environment that they can only access, and will no longer significantly encrypt the upload to a third-party cloud storage service provider. Of course, quantum computing must be able to drive the development of encryption technology. However, at present, the comparison between the spear and the shield, under the influence of the large government agencies, should be that decryption technology has the upper hand and is more likely to flow into civilian use. Quantum encryption technology is still dominated by government agencies. So from a point of view, the emergence of quantum computing is not a good news for the industry providing cloud storage services. Of course, as a programmer, if you can understand and even design a reliable quantum encryption algorithm, you may soon become a hot favorite in the IT industry, and it is not impossible even to be chased by a government agent.

What is the ultimate realization of quantum computing?

One of the ultimate goals of quantum computing research is to make and apply a Universal Quantum computer. With the current design concept, it would make sense to be able to handle at least hundreds of qubits. IBM's current 5-qubit computing service is still far from this goal. General physical quantum computers can refer to "The Physical Implementation of Quantum Computation" (http://arxiv.org/abs/quant-ph?0002077).

There are many physical implementations on the hardware, such as:

Photonics

Nuclear magnetic resonance

QED cavity

Quantum dots

Redberg atom

Ion trap

Josephson junction

And so on to achieve.

Where is the IBM cow compared to the D-wave quantum computer?

The famous D-wave generation 1 and 2 generations use the Josephson junction.

NASA, CIA and Google all purchased D-wave for related research. Oxford University, together with Rocket Martin and Nokia, has built a research center for quantum artificial intelligence based on the D-wave model. D-Wave was questioned because of its limited application scenario. The current design is not a general-purpose quantum computer.

IBM is developing a general-purpose quantum computer based on quantum logic gates, so there is no problem with generality, and all quantum algorithms can run.

In addition, IBM also completed two very important breakthroughs.

One is to detect two kinds of quantum errors at the same time : 1. bit-flip, 2. phase-flip. This greatly enhances the stability of the sub-computer.

Dirac, the simplest single qubit, denotes: Psi>=a|0>+b|1> , where a and b are the coefficients of the two ground states. Other pairs of qubit ground states are |+> and |->, |spin+> and |spin->etc. So it can also be written as |Psi>=a|+>+b|-> or |Psi>=a|spin+>+b|spin->. The orthogonal basis depends mainly on the physical implementation of the quantum system. For example, The polarization of photons, the spin of particles, and so on, are no longer in-depth here.

A qubit is an arbitrary superposition of two standard orthogonal bits 0 and 1. A and b satisfy the normalization condition, so there is a phase freedom between a and b. If the phase is disturbed during the quantum calculation, the flip is the phase-flip. A bit-flip is an unexpected change to 0 during an operation, or 1 accidentally becomes 0. Ideally, there will be no error in quantum computing. However, due to the environmental noise (mainly thermal and electromagnetic radiation), the quantum system is subject to environmental disturbances. Only in the environment of zero field and absolute zero can there be an ideal state of quantum computing. D-wave works at 20mk (273.13 degrees below zero). IBM also uses a superconducting chip. The operating temperature is 15mk (minus 273.135 degrees, only 0.015 degrees higher than the absolute zero -273.15 degrees).

Previous studies could only measure one of two errors and could not do EC (error correction). Today IBM solves this problem (http://spectrum.ieee.org/tech-talk/computing/hardware/ibm-shows-first-full-error-detection-for-quantum-computers).

The second is that IBM offers the best scalability ever. Of course there should be new issues in the implementation of actual hardware development . IBM's next goal should be to add qubits to 50 to 100. In the future, more research and development resources will be needed.

Incidentally, here is a clear clarification of many media misconceptions about qubits and their misunderstandings about quantum computing: for the advantages of quantum computing, the common explanation in the media is that the 0,1 binary values ​​used by our commonly used computers are compared. Quantum computers can store information between 0 and 1 for each qubit. This is an assumption of course, this is not an essential advantage of quantum computers at all:

It is obvious that we can characterize any continuous value between 0 and 1 just like the analog circuit composed of resistors and capacitors. So the essential difference is not the infinite possibilities of the values ​​carried by the bits, but the properties of the quantum superposition of bit information. For multi-bit operations, the advantages of quantum computers can be clearly demonstrated: all bits can perform logical operations at the same time, which is not possible with traditional electronic computers.

For multi-bit quantum systems, the qubit state of the entire system is quantitatively predictable, and individual qubits cannot be determined.

To give a simple example to illustrate the superposition and correlation of this quantum state - the very common Hadamard Gate that is also used in the tutorial of IBM Quantum Computing Services:

The function of Hadamard Gate is to convert the input α0|0⟩+α1|1⟩ to the output 2^{-1/2}(α0+α1)|0⟩+2^{-1/2}(α0-α1) |1⟩. In other words, Hadamard Gate is the "halfway" state in which the classical states |0⟩ and |1⟩ are converted to |0⟩ and |1⟩.

The key point is that this operation, even if the Hadamard gate operation is performed on only the first of the n qubits, all 2^{n} coefficients will change. The "parallel" operation here is ensured by the physical nature of quantum mechanics, not the "parallel/multithreaded" multi-core multi-device in many media.

Back to IBM's quantum computing laboratory hardware, below are two screenshots from the official website video:

Figure 1 shows an open dilution refrigerator. The temperature at the bottom of the refrigerator is the lowest, which is as low as 15mK above the absolute zero, in order to maintain the superconducting state of the superconducting material in the chip and to process the quantum information.

Figure 2 shows the gas processing system of the refrigerator . The panel shows the valve and the pump switch. The gas used in the refrigerator is Helium-3, a helium isotope.

After watching so many tall and expensive things, let's take a look at IBM's trial services for enthusiasts.

The following figure shows the trial accounts that have been applied. Following are some of the experiments that were followed by their User Guide.

The first part (The IBM Quantum Experience) is for everyone to introduce the world's first cloud-based quantum computing services.

The second part (The Weird and Wonderful World of the Qubit) is to introduce basic qubits and common sense

The third part (Multiple Qubits, Gates, and Entangled States) demonstrates the complexity and sophistication of multiple qubits through four small courses.

The fourth part (Quantum Algorithms) gives a more in-depth introduction to the wonders of the quantum world and introduces quantum algorithms that can be used for programming.

The fifth part (Quantum Error Correction) describes how to use quantum entanglement correction

The sixth part (FAQ) is the answer to common questions.

There is a small bug icon at the bottom right of the page to help users feedback various bu

The IBM official introduction video uses the Grover's Search algorithm as an example. Here I give another example with the Deutsch-Jozsa algorithm. After all, the physical model of this example can correspond to double-slit interference in optics, which looks particularly cordial.

Introduction to Deutsch-Jozsa Algorithm

The Deutsch-Jozsa quantum algorithm is the first example to demonstrate that quantum algorithms can bypass the dilemma of classical algorithms. This algorithm demonstrates that allowing the quantum amplitude to take positive and negative values, unlike the traditional probability that the probability must always be non-negative.
The Deutsch-Jozsa quantum problem is defined as follows. Consider a function f(x) that returns 0 or 1 for the input n bits x.

Suppose we make sure that f(x) is either a constant function, its return value is a constant c, c∈{0,1} for all inputs x, or f(x) is a balance function, and it is input to any 0,1 Take half the value. Our goal is to determine if f(x) is a constant function or a balance function with as few attempts as possible. The traditional algorithm requires 2^(n-1) + 1 calculations in the worst case. Using the Deutsch-Jozsa quantum algorithm, this problem can be solved with only one operation.

To understand how the Deutsch-Jozsa quantum algorithm works, let us first consider a typical interference experiment: particles that behave like waves, such as photons, can travel from a source detector array through two or more paths. It is observed that the area where the particle appearance probability is large is the area where the incident wave has the same phase when it arrives.

Imagine we can create an interference experiment with 2^n detectors and 2^n possible paths from the source to each detector. We mark them as n-bit input x- and n-bit detectors y, respectively. Further assume that the accumulated phase of x along the path of the detector is equal to C(-1)^(f(x)+x+y), where

X⋅y=Σi= xiyi

It is a binary inner product (point multiplication), and C is a normalization coefficient. The probability of observing the appearance of particles in detector y can be calculated by accumulating the square of the absolute value of the amplitude x of all paths reaching y:

PR(y) = |CΣx(-1)^(f(x)+x⋅y)| ^2

The normalized condition ΣyPr(y) = 1, then C = 2^(-n). Next we calculate the probability spectrum of the particle observed by the detector Y = 0^N (Y = 0^n) (all zero strings). We have Pr(Y = 0^n) = | 2^(-n)Σ(-1)f(x)|^ 2

If the function f(x) = c is a constant function, we will get the spectrum Pr(Yy = 0^n) = |(-1)^c |^ 2 = 1. And when f(x) is a balance function, we get Pr(y = 0^n) = 0, because all items whose sum exceeds x cancel each other out.

Therefore, we can use only one experiment to determine if f(x) is a constant or a balance function.

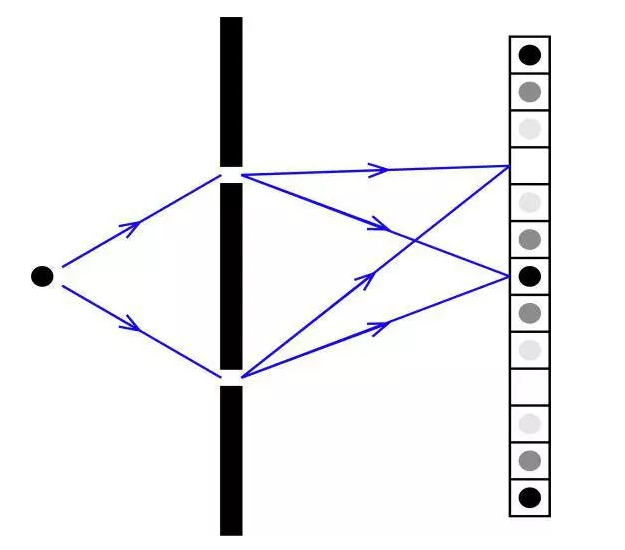
Of course, performing this experiment optically is not practical because it requires a very large optical platform! However, we can use a quantum computer to simulate this experiment, which can be achieved by using only n qubits and accessing the Oracle circuit Uf.

In fact, consider the following algorithm:

Step 1: Initialize n's all-zero state qubits | 0, ..., 0>.

Step 2 Apply Hagamard Gate H to each qubit.

Step 3. Apply Oracle Circuit Uf.

Step 4: Repeat step 2.

Step 5: Measure each qubit. Let y = (y1,...,yn) be a list of measurement results.

If f is a constant function, you will observe that y is an all-zero string. The Hagamard gate maps the input 0> to the uniformly superimposed |0> and |1>. The state of the system after the second step is 2^(-n/2)Σ|x>.

The Oracle circuit then maps this state to 2^(-n/2)Σ(-1)^f(x)|x>. Step 4 again applies the Hadamards gate, which maps the ground state |x> to a superposition state 2^(-n/2)Σ(-1)^(xy)|y>. The state of the system after completion of the fourth step is |ψ>=Σψ(y)|y>, where ψ(y)=2^(-n)Σ(-1)^(f(x)+x⋅y).
This is exactly the interference experiment we need.

The measurement in step 5 serves to detect the particles. The above result shows that if the probability y=0^n is 1, then f is a constant function. Zero, then f is a balance function. Therefore, we solve the exact solution of the Deutsch-Jozsa quantum problem with only one operation.

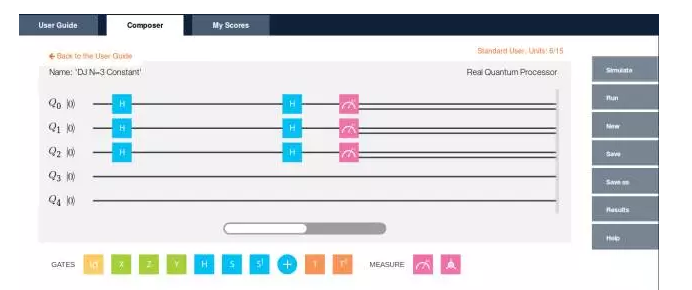
Lara mixes so much that readers without a foundation in quantum mechanics may be a bit dizzy. Then the following is the design of the actual quantum circuit:

An n=3 simulation when the function is a constant function:

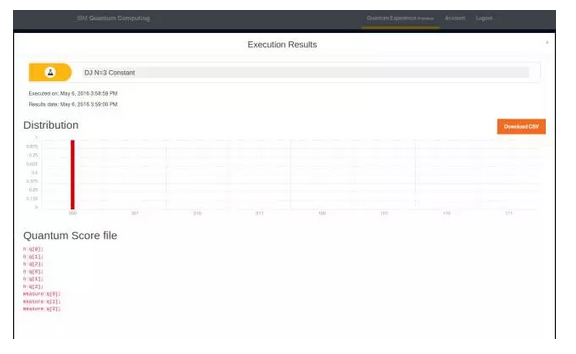
The result is the same as predicted by the theoretical analysis, ie the output is 1

Two n=3, the simulation when the function is the balance function:

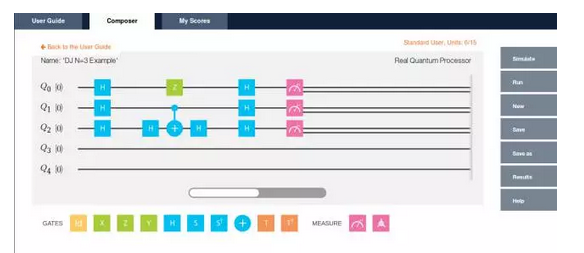
The output is the same as predicted by the theoretical analysis, ie the output is 0

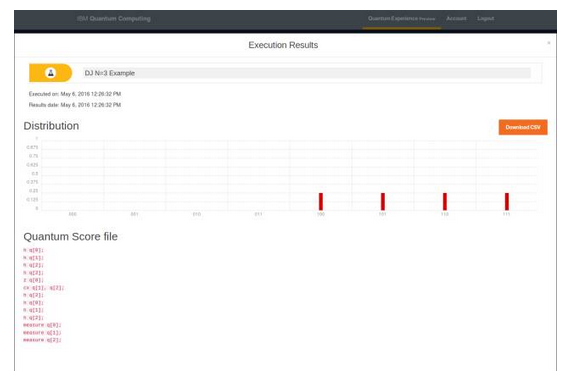
From outside evaluations: "...IBM did what it did. The service's interface is easy to use." Any student who knows about quantum computers knows how to interact with the device. ”

Cory had a trial of IBM's new service over the weekend. To his surprise, the system was fairly stable—almost every time it was tested it got the same results. This is a common phenomenon in traditional computers, but in the world of quantum computers, which are basically developed around the probability of capture, the stability of the results implies landmark progress. ”

IBM did prove one of his breakthroughs with his quantum computing platform: Simultaneous measurement of double errors greatly improves the stability of the system. In addition, the 5 qubit platform can be opened to the public, leaving us with room for imagination. How many bits of IBM can we push qubit in the short term ?

The platform provided by IBM appears to be to advertise for its R&D results and corporate brand, and the facts have indeed played a widely advertised role.

But if you really think that there is only such a little information, then you have not personally tried various quantum calculations and algorithms on the web.

If you try a little, it should be easy to find that what IBM provides is actually a two-way learning platform: Try to learn about the basic knowledge and common algorithms of quantum computing, and IBM can use it to calculate the user’s general level of understanding. .

Since each user is registered with the e-mail, he has also fought on the platform. IBM's research team will also find “advanced users” with relevant background knowledge and skilled and practical users from trial users. Maybe these users will receive IBM recruitment emails from registered emails in the near future—it's just yy. However, since people have provided this learning platform free of charge, why not use your free time to learn about it and improve your future career as a programmer?

Lei Feng Network (search "Lei Feng Network" public number attention) Note: This article has been transferred from big data talk, if you need to reprint, please contact the original author.

Gel Battery

Gel Battery,Deep Cycle Battery,Gel VRLA Battery,Acid Battery

Shenzhen Unitronic Power System Co., Ltd , https://www.unitronicpower.com