Introduce the Apriori algorithm and parse the specific strategy and steps of the algorithm, and give the Python implementation code.
Reading guide
With the hot concept of big data, the story of beer and diapers is well known. How do we find that people who buy beer often buy diapers? The Apriori algorithm used in data mining to mine frequent itemsets and association rules can tell us. This paper first introduces the Apriori algorithm, and then introduces the related basic concepts. After that, it introduces the specific strategies and steps of the Apriori algorithm in detail, and finally gives the Python implementation code.
Introduction to 1Apriori algorithm
Apriori algorithm is a classic data mining algorithm for mining frequent itemsets and association rules. A priori refers to "from the past" in Latin. When defining a problem, a priori knowledge or hypothesis is usually used, which is called "a priori". The name of the Apriori algorithm is based on the fact that the algorithm uses the a priori nature of the nature of frequent itemsets, ie all non-empty subsets of frequent itemsets must also be frequent. The Apriori algorithm uses an iterative method called layer-by-layer search, where the k-item set is used to explore the (k+1) item set. First, by scanning the database, the count of each item is accumulated, and items satisfying the minimum support degree are collected, and a set of frequent 1 item sets is found. This set is written as L1. Then, use L1 to find the set L2 of the frequent 2 item set, use L2 to find L3, and so on, until the frequent k item set can no longer be found. A complete scan of the database is required for each Lk found. The Apriori algorithm uses the a priori nature of frequent itemsets to compress the search space.
2 basic concepts
Item and item set: Let itemset={item1, item_2, ..., item_m} be a collection of all items, where item_k(k=1, 2,...,m) becomes the item. The set of items is called an itemset, and the set of items containing k items is called a k-itemset.
Transaction and transaction set: A transaction T is an item set, which is a subset of itemsets, each associated with a unique identifier Tid. Different transactions together form a transaction set D, which constitutes the transaction database discovered by the association rules.
Association rules: Association rules are implications of the form A=>B, where A and B are both subsets of itemset and are not empty sets, and A is B empty.
Support: The support for association rules is defined as follows:

among them  Represents the probability that a transaction contains the union of sets A and B (ie, containing each of A and B). Note the difference between P (A or B), which indicates the probability that a transaction contains A or B.
Represents the probability that a transaction contains the union of sets A and B (ie, containing each of A and B). Note the difference between P (A or B), which indicates the probability that a transaction contains A or B.
Confidence: The confidence of an association rule is defined as follows:

The support count of an item set: the number of transactions that contain the item set, referred to as the frequency of the item set, the support count, or the count.
Frequent itemset: If the relative support of item set I satisfies the predefined minimum support threshold (ie, the frequency of occurrence of I is greater than the corresponding minimum occurrence frequency (support count) threshold), then I Frequent itemsets.
Strong association rule: an association rule that satisfies the minimum support and the minimum confidence, that is, the association rule to be mined.
3 implementation steps
In general, the mining of association rules is a two-step process:
a. Find all frequent itemsets
b. Generate strong association rules from frequent itemsets
3.1 Mining Frequent Itemsets
3.1.1 Related definitions
Connection step: frequent (k-1) item set Lk-1 self-connection produces candidate k item set Ck
The Apriori algorithm assumes that the items in the item set are sorted in lexicographic order. If the elements (item set) of item 1 in Lk-1 are the same as the first (k-2) items of itemset2, then itemset1 and itemset2 are said to be connectable. So the result item set produced by itemset1 and itemset2 is {itemset1[1], itemset1[2], ..., itemset1[k-1], itemset2[k-1]}. The connection step is included in the create_Ck function in the code below.
Pruning strategy
Because of the a priori nature: any infrequent (k-1) item set is not a subset of the frequent k item set. Therefore, if the subset of (k-1) items of a candidate k-item set Ck is not in Lk-1, the candidate may not be frequent, so that it can be deleted from Ck, and the compressed Ck is obtained. The is_apriori function in the following code is used to determine whether the a priori property is satisfied. The create_Ck function includes a pruning step, that is, if the a priori property is not satisfied, the pruning is performed.
Delete strategy
Based on the compressed Ck, all transactions are scanned, each item in Ck is counted, and then items that do not satisfy the minimum support are deleted, thereby obtaining a frequent k item set. The delete strategy is included in the generate_Lk_by_Ck function in the code below.
3.1.2 Steps
Each item is a member of the set C1 of the candidate 1 item set. The algorithm scans all transactions, gets each item, and generates C1 (see the create_C1 function in the code below). Then count each item. Then, the unsatisfied items are deleted from C1 according to the minimum support degree, thereby obtaining the frequent 1 item set L1.
Performing a pruning strategy on the set generated by L1's own connection generates a set C2 of candidate 2 item sets, and then scans all transactions and counts each item in C2. Similarly, the unsatisfied items are deleted from C2 according to the minimum support, thereby obtaining the frequent 2 item sets L2.
Performing a pruning strategy on the set generated by L2's own connection generates a set C3 of candidate 3 item sets, and then scans all transactions and counts each item of C3. Similarly, the unsatisfied items are deleted from C3 according to the minimum support, thereby obtaining the frequent 3 item sets L3.
By analogy, a pruning strategy is executed on the set generated by Lk-1's own connection to generate a candidate k-item set Ck, and then all transactions are scanned, and each item in Ck is counted. Then, the unsatisfied items are deleted from Ck according to the minimum support degree, thereby obtaining a frequent k item set.
3.2 Generating association rules from frequent itemsets
Once you have found frequent itemsets, you can generate strong association rules directly from them. The steps are as follows:
For each frequent item set itemset, all non-empty subsets of the itemset are generated (these non-empty subsets must be frequent itemsets);
For each non-empty subset s of itemset, if 
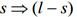
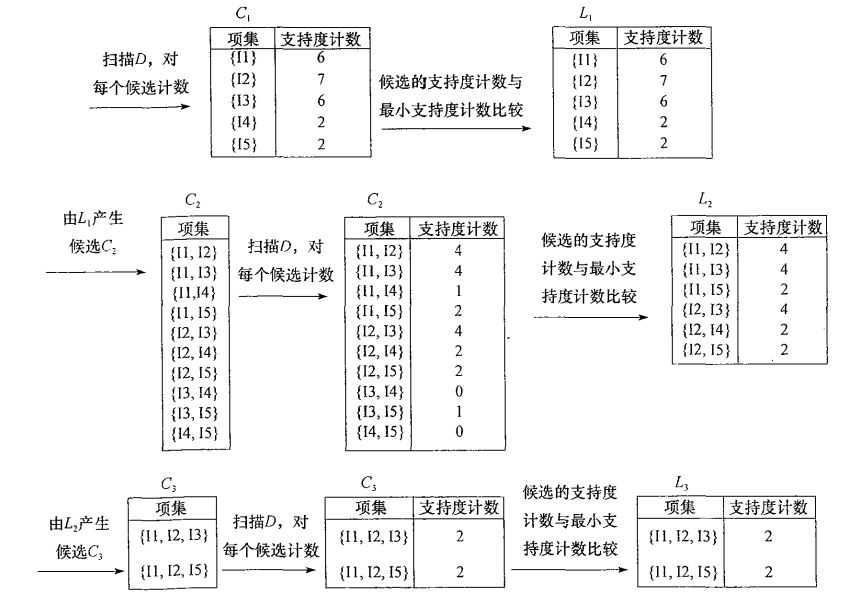
4 examples and Python implementation code
The following figure is a sample illustration of mining frequent itemsets in Data Mining: Concepts and Techniques (Third Edition).
This article writes Python code based on the sample data to implement the Apriori algorithm. The code needs to pay attention to the following two points:
Since the Apriori algorithm assumes that the items in the item set are sorted in lexicographic order, and the set itself is unordered, we need to perform set and list conversions when necessary;
Since the dictionary (support_data) is used to record the support of the item set, the item set is required as the key, and the variable set cannot be used as the key of the dictionary, so the item set should be converted to the fixed set frozenset at the appropriate time.
"""
# Python 2.7
# Filename: apriori.py
# Author: llhthinker
# Email: hangliu56[AT]gmail[DOT]com
# Blog: http://
# Date: 2017-04-16
"""
Def load_data_set():
"""
Load a sample data set (From Data Mining: Concepts and Techniques, 3th Edition)
Returns:
A data set: A list of transactions. Each transaction contains several items.
"""
Data_set = [['l1', 'l2', 'l5'], ['l2', 'l4'], ['l2', 'l3'],
['l1', 'l2', 'l4'], ['l1', 'l3'], ['l2', 'l3'],
['l1', 'l3'], ['l1', 'l2', 'l3', 'l5'], ['l1', 'l2', 'l3']]
Return data_set
Def create_C1(data_set):
"""
Create frequent candidate 1-itemset C1 by scaning data set.
Args:
Data_set: A list of transactions. Each transaction contains several items.
Returns:
C1: A set which contains all frequent candidate 1-itemsets
"""
C1 = set()
For t in data_set:
For item in t:
Item_set = frozenset([item])
C1.add(item_set)
Return C1
Def is_apriori(Ck_item, Lksub1):
"""
Judge whether a frequent candidate k-itemset satisfy Apriori property.
Args:
Ck_item: a frequent candidate k-itemset in Ck which contains all frequent
Candidate k-itemsets.
Lksub1: Lk-1, a set which contains all frequent candidate (k-1)-itemsets.
Returns:
True: satisfying Apriori property.
False: Not satisfieding Apriori property.
"""
For item in Ck_item:
sub_Ck = Ck_item - frozenset([item])
If sub_Ck not in Lksub1:
Return False
Return True
Def create_Ck(Lksub1, k):
"""
Create Ck, a set which contains all all frequent candidate k-itemsets
By Lk-1's own connection operation.
Args:
Lksub1: Lk-1, a set which contains all frequent candidate (k-1)-itemsets.
k: the item number of a frequent itemset.
Return:
Ck: a set which contains all all frequent candidate k-itemsets.
"""
Ck = set()
len_Lksub1 = len(Lksub1)
list_Lksub1 = list(Lksub1)
For i in range(len_Lksub1):
For j in range(1, len_Lksub1):
L1 = list(list_Lksub1[i])
L2 = list(list_Lksub1[j])
L1.sort()
L2.sort()
If l1[0:k-2] == l2[0:k-2]:
Ck_item = list_Lksub1[i] | list_Lksub1[j]
# pruning
If is_apriori(Ck_item, Lksub1):
Ck.add(Ck_item)
Return Ck
Def generate_Lk_by_Ck(data_set, Ck, min_support, support_data):
"""
Generate Lk by executing a delete policy from Ck.
Args:
Data_set: A list of transactions. Each transaction contains several items.
Ck: A set which contains all all frequent candidate k-itemsets.
Min_support: The minimum support.
Support_data: A dictionary. The key is frequent itemset and the value is support.
Returns:
Lk: A set which contains all all frequent k-itemsets.
"""
Lk = set()
Item_count = {}
For t in data_set:
For item in Ck:
If item.issubset(t):
If item not in item_count:
Item_count[item] = 1
Else:
Item_count[item] += 1
T_num = float(len(data_set))
For item in item_count:
If (item_count[item] / t_num) >= min_support:
Lk.add(item)
Support_data[item] = item_count[item] / t_num
Return Lk
Def generate_L(data_set, k, min_support):
"""
Generate all frequent itemsets.
Args:
Data_set: A list of transactions. Each transaction contains several items.
k: Maximum number of items for all frequent itemsets.
Min_support: The minimum support.
Returns:
L: The list of Lk.
Support_data: A dictionary. The key is frequent itemset and the value is support.
"""
Support_data = {}
C1 = create_C1(data_set)
L1 = generate_Lk_by_Ck(data_set, C1, min_support, support_data)
Lksub1 = L1.copy()
L = []
L.append(Lksub1)
For i in range(2, k+1):
Ci = create_Ck(Lksub1, i)
Li = generate_Lk_by_Ck(data_set, Ci, min_support, support_data)
Lksub1 = Li.copy()
L.append(Lksub1)
Return L, support_data
Def generate_big_rules(L, support_data, min_conf):
"""
Generate big rules from frequent itemsets.
Args:
L: The list of Lk.
Support_data: A dictionary. The key is frequent itemset and the value is support.
Min_conf: Minimal confidence.
Returns:
Big_rule_list: A list which contains all big rules. Each big rule is represented
As a 3-tuple.
"""
Big_rule_list = []
Sub_set_list = []
For i in range(0, len(L)):
For freq_set in L[i]:
For sub_set in sub_set_list:
If sub_set.issubset(freq_set):
Conf = support_data[freq_set] / support_data[freq_set - sub_set]
Big_rule = (freq_set - sub_set, sub_set, conf)
If conf >= min_conf and big_rule not in big_rule_list:
# print freq_set-sub_set, " => ", sub_set, "conf: ", conf
Big_rule_list.append(big_rule)
Sub_set_list.append(freq_set)
Return big_rule_list
If __name__ == "__main__":
"""
Test
"""
Data_set = load_data_set()
L, support_data = generate_L(data_set, k=3, min_support=0.2)
Big_rules_list = generate_big_rules(L, support_data, min_conf=0.7)
For Lk in L:
Print "="*50
Print "frequent " + str(len(list(Lk)[0])) + "-itemsetssupport"
Print "="*50
For freq_set in Lk:
Print freq_set, support_data[freq_set]
Print "Big Rules"
For item in big_rules_list:
Print item[0], "=>", item[1], "conf: ", item[2]
The screenshot of the code running result is as follows:

Watch Screen Protector features a stretchable and retractable TPU Screen Protector that resists air bubbles and fingerprints on your device's screen and provides maximum protection for your device from scratches. The Hydrogel Film repairs screen scratches on its own and is ideal for curved curved screens.
Full Coverage: The soft material matches the edges of the watch screen well. Full coverage provides better protection and looks very discreet.
Oleophobic and waterproof: The oleophobic waterproof transparent layer can prevent the residue of sweat and grease, resist fingerprints, and keep the phone screen as new as ever.
Sensitive touch: only 0.14mm thick ultra-thin protective layer will not interfere with touch screen commands, your touch screen can still operate 100% normally.
If you want to know more information about Smart Watch Screen Protector products, please click the product details to view the parameters, models, pictures, prices and other information of Watch Screen Protector products.
Whether you are a group or an individual, we will do our best to provide you with accurate and comprehensive information about Watch Hydrogel Screen Protectors!
Watch Screen Protector, Watch Hydrogel Screen Protector,Smart Watch Screen Protector,Watch Protective Film,Apple Watch Screen Protector,Watch Screen Protector Cover
Shenzhen Jianjiantong Technology Co., Ltd. , https://www.jjtphonesticker.com
