Understanding these basic analytics techniques will bring more benefits to project development and data understanding.
No matter how you look at the research work of data scientists, the importance of analyzing, organizing, and combing data cannot be easily ignored. The Glassdoor website collected a large number of feedback from employers and employees and found that data scientists ranked first in the "25 best jobs in the United States." Despite this laurel, the work that needs to be studied by data scientists is constantly being added. With the increasing use of technologies such as machine learning, and the increasing popularity of researchers and engineers and companies in the hottest areas such as deep learning, data scientists will continue to stand at the forefront of technological innovation and lead the technological transformation of the times. .
Therefore, they need to systematically study statistical machine learning, which is derived from statistics and functional analysis, and combines multiple disciplines such as information theory, optimization theory, and linear algebra. Although powerful programming skills are important to data scientists, data scientists are not exactly software engineers. In fact, mastering Python is enough for them. What really matters is the ability to have both programming, statistics, and critical thinking.
As Josh Wills puts it: “Data scientists are better at programmers than statistics, and statisticians are good at programming.†Many software engineers want to transform data scientists, but they blindly use machine learning frameworks such as TensorFlow or Apache Spark to process data, but Ignore the knowledge of statistical theory behind it. That is, statistical learning theory, the theoretical framework of machine learning, which is derived from statistics and functional analysis.
So why study statistical learning? We can only apply what we have learned if we have a deep understanding of the ideas behind different technologies. It’s only easy to make it easy, and it’s easy to get through. At the same time, it is very important to accurately evaluate the performance of a method. Not only can you know the effect of the work, but you can also know the scope of the method. In addition, statistical learning is also an exciting area of ​​research with important applications in science, industry and finance. Finally, statistical learning is a fundamental element in cultivating modern data scientists. Examples of statistical learning problem applications are as follows:
Identify risk factors for prostate cancer
Classify recordings based on log-period graphs
Predict whether you will have heart disease based on demographics, diet, and clinical measurements
Customized spam detection system
Identify handwritten zip codes
Classification of cancer in tissue samples
Establishing the relationship between salary and demographic variables in the population survey data
Before introducing the 10 commonly used statistical techniques, we need to distinguish between machine learning and statistical learning. The main differences are as follows:
Machine learning is a branch of artificial intelligence
Statistical learning is a branch of the statistical field
Machine learning is more focused on the accuracy of large-scale applications and predictions
Statistical learning emphasizes models and their interpretability, precision and uncertainty
But the difference is getting more and more blurred, and the two are often intertwined.
I have to say that marketing has made machine learning very hot.
Linear regression
In statistics, linear regression is a method of predicting a target variable by fitting the optimal linear relationship between the dependent variable and the independent variable. The best fit represents the error and minimum of the predicted output from the current linear expression and the actual observed value.
Linear regression is mainly divided into simple linear regression and multiple linear regression. Simple linear regression uses an independent variable to fit the optimal linear relationship prediction dependent variable; multivariate linear regression uses multiple independent variables to fit the optimal linear relationship prediction dependent variable.
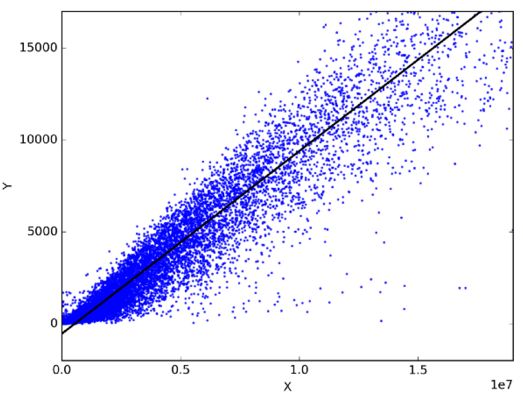
So what practical problems can linear regression be used for? In fact, arbitrarily choose two things related to daily life, you can get a linear relationship between them through linear regression models. For example, if you have data on monthly consumption, monthly income, and monthly travel times in the past three years, you can predict the monthly expenditure for the next year. You can also know whether monthly income or monthly travel has more impact on monthly consumption, and even use The equation expresses the relationship between monthly income, monthly travel times, and monthly consumption.
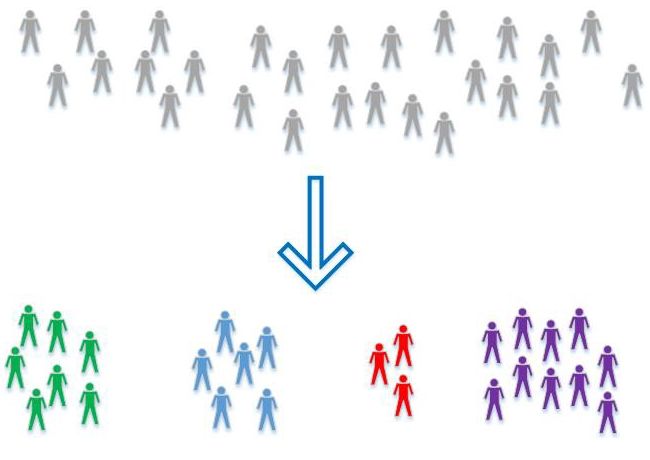
classification
Classification is a data mining technique, and dividing data sets into multiple categories can help more accurate prediction and analysis. Classification is a method for efficiently analyzing large data sets. Typical representatives are Logistic Regression analysis and Discriminant Analysis.
Logistic regression analysis is suitable for regression analysis when the dependent variable is a binary class. Like all regression analyses, logistic regression is also a predictive analysis. Logistic regression is used to describe the data and to explain the relationship between binary dependent variables and one or more descriptive independent variables such as nominal, ordinal, interval, or ratio levels. The types of problems that are suitable for logistic regression are:
Whether the weight exceeds one pound per standard weight or one pack per cigarette per day has an effect on the probability of lung cancer (yes or no).
Whether calorie intake, fat intake, and age have an effect on heart disease (yes or no).
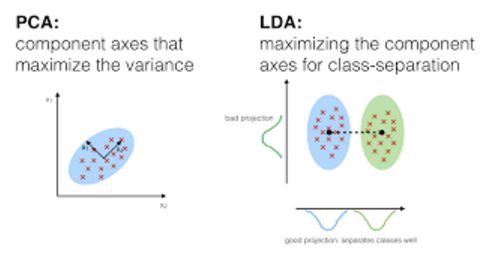
In the discriminant analysis, two or more known sets, clusters or groups can be used as prior knowledge of the classification, and the new observations can be divided into corresponding categories according to the measured features. Discriminant analysis models the predictive factors X in each class separately, and then converts them into probability estimates based on the X-values ​​that can be obtained from the corresponding categories based on Bayes' theorem. Such models can be either linear discriminant analysis or quadratic discriminant analysis.
Linear Discriminant Analysis linear discriminant analysis, which calculates the "discriminating score" for each observation by linear combination of independent variables, and classifies the response variable Y category. It assumes that observations within each category are subject to a multivariate Gaussian distribution with the same variance for each category.
Quadratic Discriminant Analysis provides another method. Like LDA, QDA also assumes that each type of observation from Y is subject to a Gaussian distribution. But unlike LDA, QDA assumes that each category has its own covariance matrix, which means that the variance of each category is different.
Resampling method
The resampling method is to repeatedly extract samples from the original data samples, which is a nonparametric method of statistical inference. Resampling does not use a general distribution table to approximate the value of probability p, but instead generates a unique sample distribution based on the actual data. This adoption distribution is generated by empirical methods rather than analytical methods, which can obtain unbiased estimates based on unbiased samples of all possible outcomes of the data. In order to understand the concept of resampling well, we need to understand Bootstrapping and Cross-Validation:
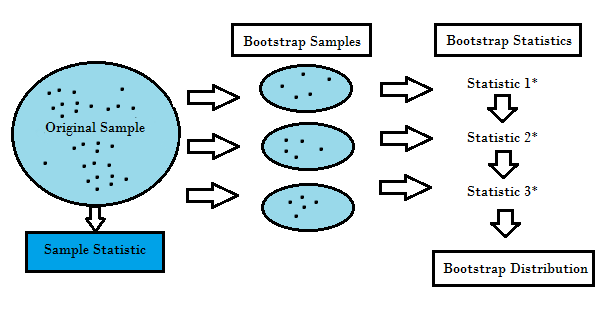
Bootstrapping is a performance and integration method that helps to validate predictive models in many cases, estimating model bias and variance. It does this by putting back the raw data and putting "unselected" data points as test cases. We can do this several times and then use the average as our estimate of the performance of the model.
Cross validation cross-validation validates model performance by dividing training data into k parts, using the k-1 part as the training set and the rest as the test set. After repeating different k times, the average of the k scores is taken as the performance estimate of the model.
Usually for linear models, the ordinary least squares method is the main criterion when fitting data. The next three methods can provide better prediction accuracy and model interpretability for linear model fitting.
Subset selection
The main purpose of subset selection is to pick out the p predictors most relevant to the problem and then fit the model using the subset features and least squares.
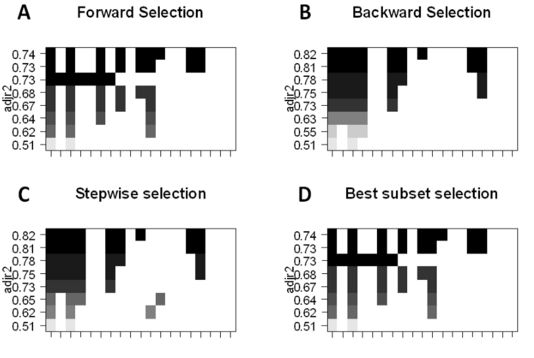
For the selection of the best subset, we can fit the ordinary least squares regression for each combination of p predictors, and then observe the fitting results of each model. The algorithm is divided into two phases: (1) fitting all models containing k predictors, where k is the maximum length of the model; and (2) selecting a single model using cross-validation prediction loss. It is important to remember that it is not possible to simply use the training error to estimate the fit of the model. It is also important to verify the error of the set or test set, as RSS and R^2 will increase monotonically as the variable increases. The best way to do this is to select the model by cross-validating by selecting the highest R^2 and lowest RSS in the test set.
The forward selection is forwarded, and a smaller subset of p predictors can be selected. The algorithm begins with a model that does not contain predictors, and then gradually adds predictors to the model until all predictors are included in the model. The order in which the predictors are added is determined by the degree to which the different variables fit the performance of the model, and new predictors are added until the cross-validation error has not changed significantly.
The backward stepwise selection, in contrast to the forward stepwise selection, first includes all p predictors, and then iteratively removes the least useful predictor.
In the hybrid approach, the body follows the forward stepwise approach, but after adding each new variable, the method may also remove variables that are not useful for model fitting.
Feature reduction technique
The feature reduction technique uses all p predictors to model, however, the coefficient representing the importance of the predictor will shrink toward zero with the least squares error, which is also called regularization, which is designed to reduce variance to prevent Over-fitting of the model. Commonly used reduction factor methods are lasso (L1 regularization) and ridge regression (L2 regularization).
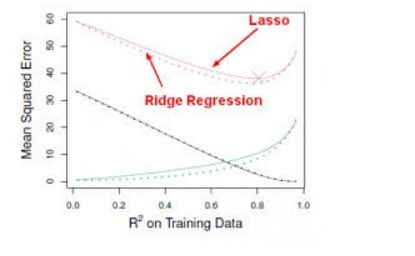
Ridge regression is similar to the least squares method in that it seeks to reduce the coefficient estimation of RSS, but it adds the penalty term to the loss function (that is, the optimization target), so that the size of the coefficient will be considered in the process of training parameters. We don't need mathematical analysis to see that Ridge regression is very good at shrinking features into the smallest subspace. For principal component analysis PCA, Ridge regression can be used to project data into a low-dimensional space and shrink the components of the lower variance in the coefficient space while preserving the components with higher variance.
However, Ridge regression has a disadvantage. The final model needs to contain all p predictors. This is because although the penalty will make the coefficients of many predictors close to zero, it must not equal zero. Although this has no effect on the accuracy of the prediction, the results of the model are more difficult to interpret. The Lasso method overcomes this shortcoming well because it forces the coefficients of some predictors to zero when s is small enough. When s = 1, it is like a normal OLS regression, and when s approaches 0, the coefficient will shrink to zero. So Lasso regression is also a good way to perform variable selection.
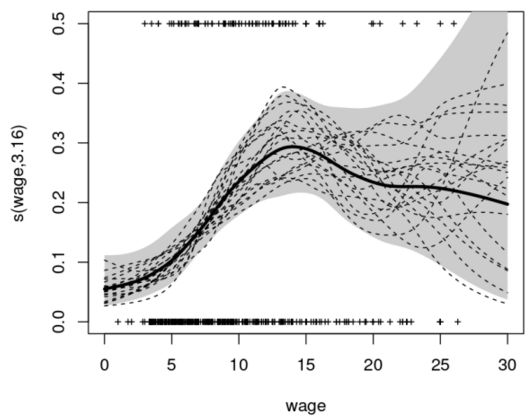
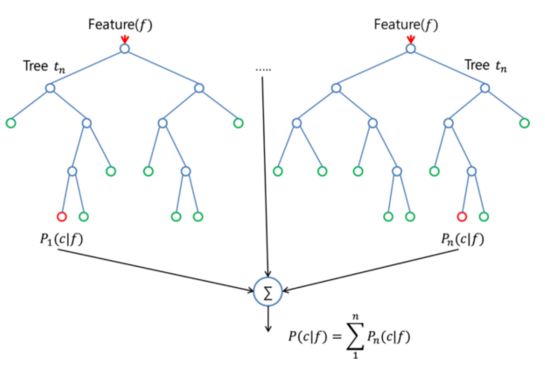
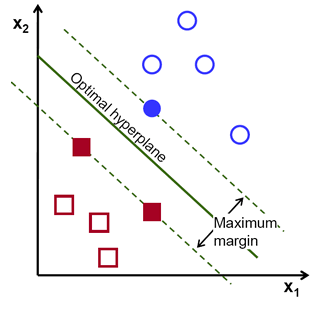
Dimensionality reduction (dimension reduction)
Dimensionality reduction will simplify the p + 1 coefficient estimation problem to the M + 1 coefficient estimation problem, where M Principal Components Regression is a method of finding low-dimensional feature sets from a large number of variables. The first principal component in the data means that the observed data changes the most along the direction of the variable, that is, if the p main components are used to fit the data, the first principal component must be the closest. The line of data distribution. The second principal component is a linear combination of variables that are not related to the first principal component, and has the largest variance under the constraint. The main idea is that the principal component can use the linear combination of the data in mutually perpendicular directions to get the largest variance. Based on this method, we can also get more information from the data by combining the effects of related variables. After all, in the conventional least squares method, one of the related variables needs to be discarded. Since the PCR method requires an optimal linear combination of X. Since the output Y corresponding to X has no effect on the calculation of the principal component direction, that is to say, these combinations (directions) are obtained by unsupervised methods, there is no guarantee that these directions are the optimal representation of the predictor and cannot be guaranteed. Optimal predictive output. Partial least squares (PLS) is an alternative to PCR and is a supervised method. Similar to PCR, PLS is also a dimensionality reduction method, which first extracts a new smaller feature set (linear combination of original features) and then fits the original model to a new M feature by least squares method. The linear model evaluates whether the feature set is the optimal linear combination of Y by predicting the model error. Nonlinear model In statistics, nonlinear regression is a form of regression analysis that models observation data by nonlinear combination of model parameters (depending on one or more independent variables) and uses successive approximation to fit the data. Here are a few important techniques for dealing with nonlinear models: Step function, the variable is a real number, which can be written as a finite linear combination of the utility functions of the interval. In layman's terms, a step function is a piecewise constant function with only a finite part. A piecewise function is defined by a plurality of sub-functions, and each sub-function is defined on a determined interval. Segmentation is actually a representation of a function, not a function's own characteristics, but it can also be used to describe the function itself with additional qualifications. For example, a piecewise polynomial function is a function that is a polynomial on each sub-definition, where each polynomial may be different. A spline is a special function defined by polynomial segmentation. In computer graphics, a spline curve is a piecewise polynomial parameterized curve. Spline curves are common because of their simple structure, ease of evaluation, and high precision, as well as the ability to approximate complex curves through curve fitting and interactive curve design. The generalized additive model is a generalized linear model in which the linear predictor linearly depends on the unknown smoothing function of some predictor variables, and its main function is to infer these smoothing functions. Tree based approach Tree-based methods can be used for regression and classification problems, which layer or segment the predictor space into simple regions. Since the set of splitting rules of the predictor space can be summarized as a tree, it is also called a decision tree method. The following methods are several different trees that can be combined to vote for a unified prediction. Bagging can reduce the variance of the prediction by generating additional training data from the raw data (by combining and repetitively generating multiple pieces of data of the same size as the original data), but it does not improve the predictive power of the model. Boosting is a method of calculating output, using multiple different models, and then using a weighted average method to average the results. The weight of these methods is generally combined with the advantages of each method. In addition, finer parameters can be fine-tuned for better predictive power for broader input data. The random forest algorithm is actually similar to the bagging algorithm. It also extracts random bootstrap samples from the training set. However, in addition to the bootstrap sample, a random subset of features can be extracted to train a single tree; in bagging, all features need to be provided for each tree. Since feature selection is random, each tree is more independent than the conventional bagging algorithm, which usually results in better predictive performance (thanks to better variance-deviation tradeoffs). Since each tree only needs to learn a subset of features, the speed is also improved. Support Vector Machines Support Vector Machine (SVM) is a commonly used supervised learning classification technique. In layman's terms, it looks for the optimal hyperplane of two types of point sets (hyperplane, which is a line in 2D space, a face in 3D space, and a hyperplane in high-dimensional space. The hyperplane is n-dimensional in n-dimensional space) 1 dimensional subspace). This hyperplane makes the interval between the two types of point sets the largest, which is essentially a constraint optimization problem, which maximizes the interval under certain constraints, thus achieving perfect classification of data. "Support Vectors" are those that support the hyperplane, or the data points closest to the hyperplane. In the image above, the blue filled circle and the two filled squares are the support vectors. During use, when the two types of data are linearly inseparable, the data points can be projected into the high-dimensional space by the kernel function, making the data linearly separable. Multi-classification problems can also be broken down into multiple "one-versus-one" or "one-versus-rest" two-class problems. Unsupervised learning Supervised learning is a large part of machine learning, in which data classification is known. When data classification is unknown, another technique is needed, unsupervised learning, which requires itself to discover patterns in the data. Clustering (clustring) is a typical unsupervised learning, and data is divided into multiple clusters based on relevance. Here are some of the most common unsupervised learning algorithms: Principal Component Analysis Principal Component Analysis: A low-dimensional representation of a data set can be generated by preserving a linear combination of features with maximum variance and irrelevant features. It also helps to understand hidden variable interactions in unsupervised learning. k-Means clusteringk Mean clustering: It belongs to the hard clustering algorithm, which divides it into k different clusters according to the distance from the data to the cluster center. Hierarchical clustering: Since the k-means algorithm always has the problem of K value selection and initial cluster center point selection, these problems will also affect the clustering effect. In order to avoid these problems, we can choose another more practical clustering algorithm, which is the hierarchical clustering algorithm. As the name suggests, hierarchical clustering is clustering layer by layer. It can divide large clusters from top to bottom, called splitting method. It can also aggregate small categories from bottom to top, called condensing. The method; but the more commonly used is the method of cohesion from bottom to top. These are some of the statistical techniques that help data scientists understand the basics of data. Understanding these basic analysis techniques will bring more benefits to the development of the project and the understanding of the data, and the abstraction and operation of the data will become easier. I hope this article will help the small partners bring some new gains in understanding the data science. Compared with large complex thin - wall castings, civil products have lower requirements on casting quality. However, for the latter, shorten the production cycle, improve the production efficiency of the problem becomes more prominent. The gelation process of common silica sol mainly depends on the dehydration and drying of silica sol, which takes longer time than the gelation of chemical hardening ethyl silicate. Ethyl silicate shell using ammonia dry each layer can be completed in 2h, and the final hardening of silica sol generally takes more than 12h, for some deep holes and other difficult to dry parts of the need for a longer time. At the same time, because the Investment Casting shell needs to be made in layers, each layer needs to be fully dried, to ensure that the lower shell immersion coating will not cause the problem of remelting off, and immersion coating itself, water will be immersed in the dried shell, resulting in a long overall drying cycle. It is a schematic diagram of the production cycle of silica sol shell investment casting under general conditions. As can be seen from the figure, shell making time accounts for more than 50% of the whole casting production cycle. To shorten the delivery time and shell making cycle is the core of the problem. The key factors to shorten the shell-making period can be divided into two aspects: internal cause and external cause. The main internal cause is the characteristics of the binder, and the external cause is the drying condition. Silica Sol Casting industry in China is developing rapidly and its application is also very extensive. Tianhui Machine Co.,Ltd , https://www.thcastings.com